Matrix Completion 矩阵补充

最简单的一种方法，实际效果不好

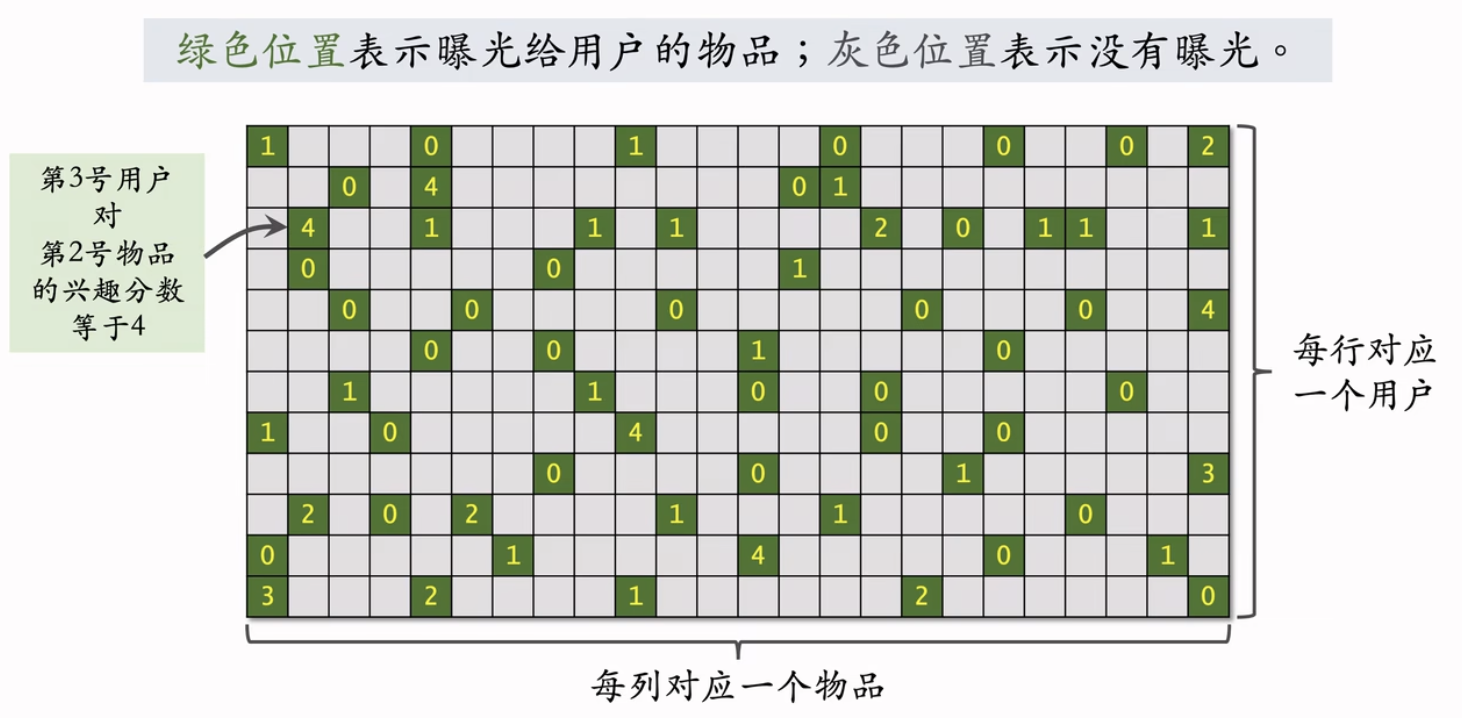
数据集

• 数据集：(用户D,物品D,兴趣分数) 的集合，记作$\Omega=\{(u,i,y)\}$。
• 数据集中的兴趣分数是系统记录的，比如：
  • ·曝光但是没有点击→0分
  • ·点击、，点赞、收藏、转发→各算1分
  • ·分数最低是0，最高是4。

训练

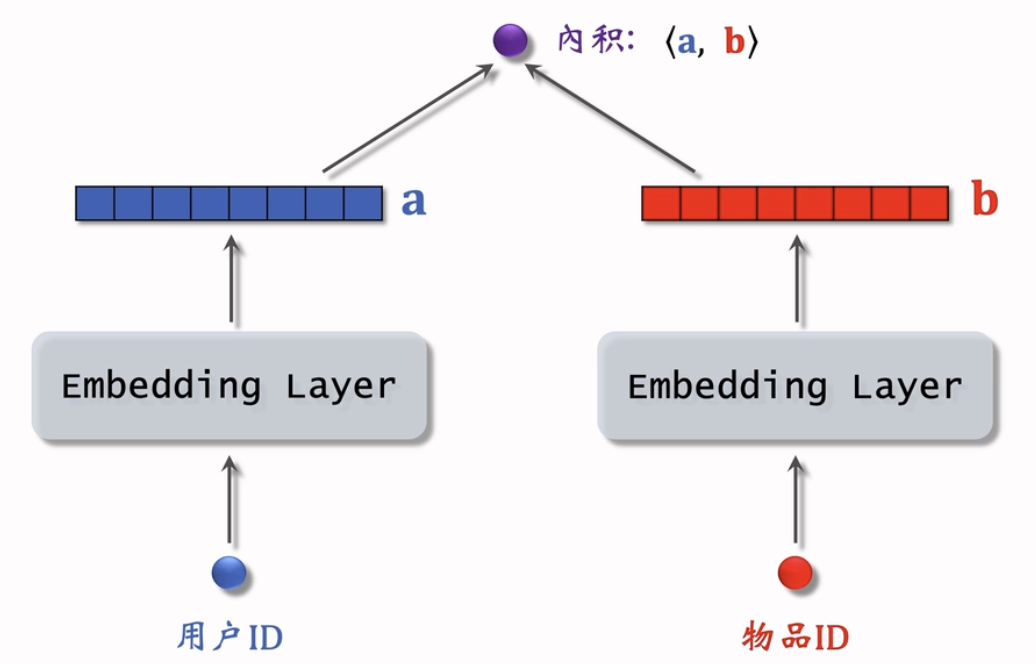
• 把用户ID、物品ID映射成向量
  • ·第u号用户→向量$a_u$
  • ·第i号物品→向量$b_i$
• 求解优化问题，得到参数A和B。
  • $\min\limits_{A,B}\sum_{(u,i,y)\inΩ}(y - <a_u,b_i>)^2.$

缺点

在实践中效果不好…

缺点1：仅用ID embedding,没利用物品、用户属性。

• ·物品属性：类目、关键词、地理位置、作者信息。
• ·用户属性：性别、年龄、地理定位、感兴趣的类目。
• ·双塔模型可以看做矩阵补充的升级版。

缺点2：负样本的选取方式不对。

• ·样本：用户一物品的二元组，记作(u,i)。
• ·正样本：曝光之后，有，点击、交互。（正确的做法）
• ·负样本：曝光之后，没有点击、交互。（错误的做法)

缺点3：做训练的方法不好。

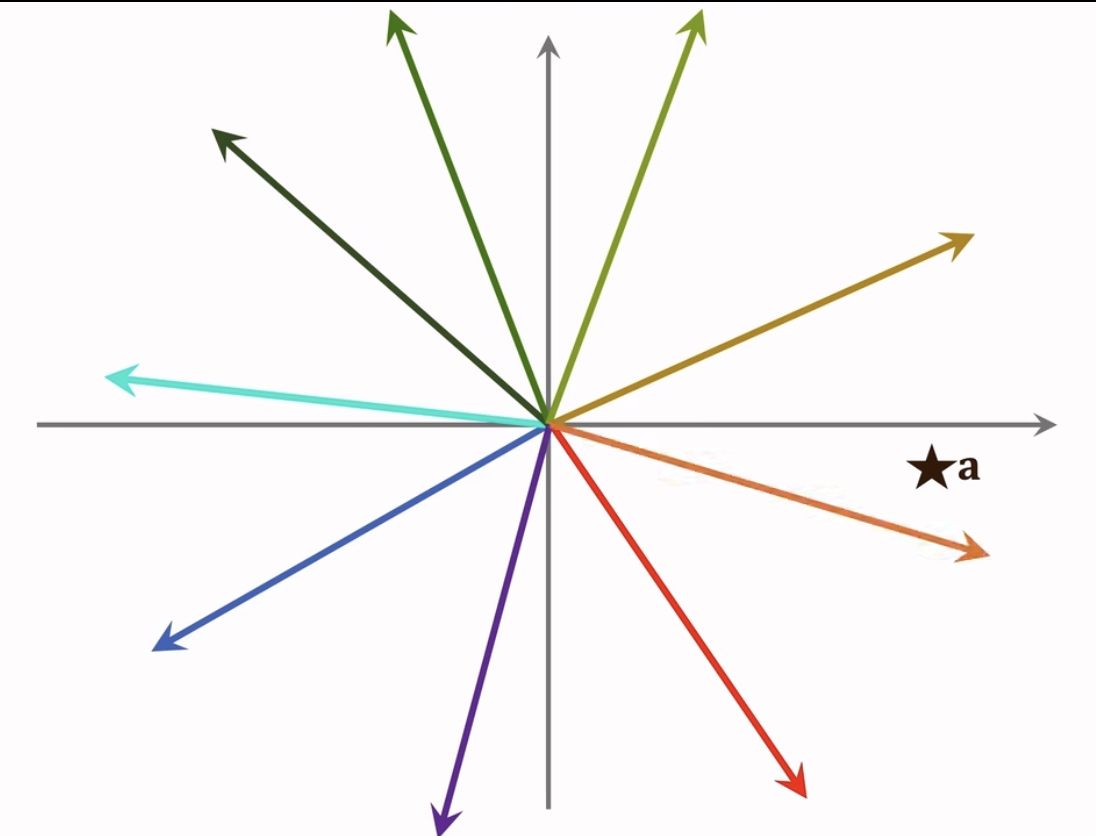
• 內积$<a_u,b_i>$不如余弦相似度。
• 用平方损失（回归），不如用交叉熵损失（分类)。

模型存储

1. 训练得到矩阵A和B。
   • ·A的每一列对应一个用户。
   • ·B的每一列对应一个物品。
2. 把矩阵A的列存储到key-value表。
   • ·key是用户ID,value是A的一列。
   • ·给定用户ID,返回一个向量（用户的embedding)o
3. 矩阵B的存储和索引比较复杂。

线上服务

把用户ID作为key,查询key-value表’得到该用户的向量，记作a。

最近邻查找：查找用户最有可能感兴趣的k个物品，作为召回结果。

• ·第i号物品的embedding向量记作bio
• ·內积(a,b〉是用户对第i号物品兴趣的预估。
• ·返回內积最大的k个物品。

如果枚举所有物品，时间复杂度正比于物品数量

近似最近邻查找（Approximate Nearest Neighbor Search）

支持最近邻查找的系统

• ·系统：Milvus、Faiss、HnswLib、等等。
• ·衡量最近邻的标准：
  • ·欧式距离最小（L2距离）
  • ·向量內积最大（內积相似度)
  • ·向量夹角余弦最大（cosine相似度）
    • 针对不支持cosine的系统，只需要把向量做归一化，然后内积就等于cosine了

---

• 把物品ID、用户ID做embedding，映射成向量。
• 两个向量的內积$<a_u,b_i>$作为用户u对物品i兴趣的预估。
• 让$<a_u,b_i>$拟合真实观测的兴趣分数，学习模型的embedding层参数。
• 矩阵补充模型有很多缺点，效果不好。