Permutation

Have Something to do with sequence.

247. Strobogrammatic Number II

Given an integer n, return all the strobogrammatic numbers that are of length n. You may return the answer in any order.

A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down).

static final char[][] REVERSIBLE_PAIRS = {
        { '0', '0' }, { '1', '1' },
        { '6', '9' }, { '8', '8' }, { '9', '6' }
};

public List<String> generateStroboNumbers(int i, int n) {
    if (i == 0) {
        return Arrays.asList("");
    }

    if (i == 1) {
        return Arrays.asList("0", "1", "8");
    }

    List<String> prev = generateStroboNumbers(i - 2, n);
    List<String> curr = new ArrayList<>(prev.size() * REVERSIBLE_PAIRS.length);

    for (String prevStroboNum : prev) {
        for (char[] pair : REVERSIBLE_PAIRS) {
            // We can only append 0's if it is not first digit.
            if (pair[0] != '0' || i != n) {
                curr.add(pair[0] + prevStroboNum + pair[1]);
            }
        }
    }

    return curr;
}

public List<String> findStrobogrammatic(int n) {
    return generateStroboNumbers(n, n);
}

351. Android Unlock Patterns

Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an "unlock pattern" by connecting the dots in a specific sequence, forming a series of joined line segments where each segment's endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

• All the dots in the sequence are distinct.
• If the line segment connecting two consecutive dots in the sequence passes through the center of any other dot, the other dot must have previously appeared in the sequence. No jumps through the center non-selected dots are allowed.
  • For example, connecting dots 2 and 9 without dots 5 or 6 appearing beforehand is valid because the line from dot 2 to dot 9 does not pass through the center of either dot 5 or 6.
  • However, connecting dots 1 and 3 without dot 2 appearing beforehand is invalid because the line from dot 1 to dot 3 passes through the center of dot 2.

Here are some example valid and invalid unlock patterns:

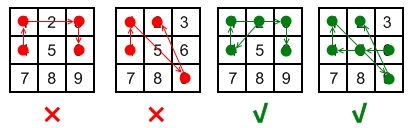
• The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence.
• The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
• The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence.
• The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

static final int[][] SINGLE_STEP_MOVES = {
        { 0, 1 }, { 0, -1 },
        { 1, 0 }, { -1, 0 }, // Adjacent moves (right, left, down, up)
        { 1, 1 }, { -1, 1 },
        { 1, -1 }, { -1, -1 }, // Diagonal moves
        { -2, 1 }, { -2, -1 },
        { 2, 1 }, { 2, -1 },
        { 1, -2 }, { -1, -2 },
        { 1, 2 }, { -1, 2 }, // Extended moves (knight-like moves)
};

static final int[][] SKIP_DOT_MOVES = {
        { 0, 2 },
        { 0, -2 },
        { 2, 0 },
        { -2, 0 }, // Straight skip moves (e.g., 1 to 3, 4 to 6)
        { -2, -2 },
        { 2, 2 },
        { 2, -2 },
        { -2, 2 }, // Diagonal skip moves (e.g., 1 to 9, 3 to 7)
};

public int numberOfPatterns(int m, int n) {
    int totalPatterns = 0;
    // Start from each of the 9 dots on the grid
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            boolean[][] seen = new boolean[3][3];
            // Count patterns starting from this dot
            totalPatterns += countPatterns(m, n, 1, i, j, seen);
        }
    }
    return totalPatterns;
}

private int countPatterns(
        int m,
        int n,
        int len,
        int i,
        int j,
        boolean[][] seen) {
    // Base case: if current pattern length exceeds n, stop exploring
    if (len > n) {
        return 0;
    }

    int validPatterns = 0;
    // If current pattern length is within the valid range, count it
    if (len >= m) {
        validPatterns++;
    }

    // Mark current dot as visited
    seen[i][j] = true;

    // Explore all single-step moves
    for (int[] move : SINGLE_STEP_MOVES) {
        int newRow = i + move[0];
        int newCol = j + move[1];
        if (isValidMove(newRow, newCol, seen)) {
            // Recursively count patterns from the new position
            validPatterns += countPatterns(
                    m,
                    n,
                    len + 1,
                    newRow,
                    newCol,
                    seen);
        }
    }

    // Explore all skip-dot moves
    for (int[] move : SKIP_DOT_MOVES) {
        int newRow = i + move[0];
        int newCol = j + move[1];
        if (isValidMove(newRow, newCol, seen)) {
            // Check if the middle dot has been visited
            int middleRow = i + move[0] / 2;
            int middleCol = j + move[1] / 2;
            if (seen[middleRow][middleCol]) {
                // If middle dot is visited, this move is valid
                validPatterns += countPatterns(
                        m,
                        n,
                        len + 1,
                        newRow,
                        newCol,
                        seen);
            }
        }
    }

    // Backtrack: unmark the current dot before returning
    seen[i][j] = false;
    return validPatterns;
}

boolean isValidMove(int i, int j, boolean[][] seen) {
    return (i >= 0 && j >= 0 && i < 3 && j < 3 && !seen[i][j]);
}

489. Robot Room Cleaner

You are controlling a robot that is located somewhere in a room. The room is modeled as an m x n binary grid where 0 represents a wall and 1 represents an empty slot.

The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API Robot.

You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is 90 degrees.

When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.

Design an algorithm to clean the entire room using the following APIs:

class Solution {
    // Going clockwise: 0: 'up', 1: 'right', 2: 'down', 3: 'left'
    private static final int[][] DIRS = { { -1, 0 }, { 0, 1 }, { 1, 0 }, { 0, -1 } };

    // Use record for immutable position coordinates
    private record Position(int row, int col) {
    }

    private Set<Position> visited = new HashSet<>();
    private Robot robot;

    private void goBack() {
        robot.turnRight();
        robot.turnRight();
        robot.move();
        robot.turnRight();
        robot.turnRight();
    }

    private void backtrack(int row, int col, int direction) {
        Position current = new Position(row, col);
        visited.add(current);
        robot.clean();

        // Explore 4 directions clockwise
        for (int i = 0; i < 4; i++) {
            int newDirection = (direction + i) % 4;
            int newRow = row + DIRS[newDirection][0];
            int newCol = col + DIRS[newDirection][1];
            Position next = new Position(newRow, newCol);

            if (!visited.contains(next) && robot.move()) {
                backtrack(newRow, newCol, newDirection);
                goBack();
            }
            // Turn robot clockwise to next direction
            robot.turnRight();
        }
    }

    public void cleanRoom(Robot robot) {
        this.robot = robot;
        backtrack(0, 0, 0);
    }
}

2184. Number of Ways to Build Sturdy Brick Wall

You are given integers height and width which specify the dimensions of a brick wall you are building. You are also given a 0-indexed array of unique integers bricks, where the ith brick has a height of 1 and a width of bricks[i]. You have an infinite supply of each type of brick and bricks may not be rotated.

Each row in the wall must be exactly width units long. For the wall to be sturdy, adjacent rows in the wall should not join bricks at the same location, except at the ends of the wall.

Return the number of ways to build a sturdy wall. Since the answer may be very large, return it modulo 109 + 7.

public int buildWall(int height, int width, int[] bricks) {
    int mod = 1000000007;

    List<Integer> buildLayer = waysOfBuildLayerRecursive(width, bricks);
    if (height == 1) {
        return buildLayer.size();
    }

    List<List<Integer>> nexts = new ArrayList<>();
    for (int i = 0; i < buildLayer.size(); i++) {
        int split = buildLayer.get(i);
        ArrayList<Integer> next = new ArrayList<Integer>();
        for (int j = 0; j < buildLayer.size(); j++) {
            int nextSplit = buildLayer.get(j);
            if ((split & nextSplit) == 0) {
                next.add(j);
            }
        }
        nexts.add(next);
    }

    int[] thisLayer = new int[buildLayer.size()];
    Arrays.fill(thisLayer, 1);

    for (int i = 1; i < height; i++) {
        int[] nextLayer = new int[buildLayer.size()];
        for (int j = 0; j < thisLayer.length; j++) {
            List<Integer> next = nexts.get(j);
            for (int nextSplit : next) {
                nextLayer[nextSplit] = (nextLayer[nextSplit] + thisLayer[j]) % mod;
            }
        }
        thisLayer = nextLayer;
    }
    int result = 0;
    for (int num : thisLayer) {
        result = (result + num) % mod;
    }
    return result;
}

private List<Integer> waysOfBuildLayerRecursive(int width, int[] bricks) {
    List<Integer> result = new ArrayList<>();
    waysOfBuildLayerRecursive(new Stack<Integer>(), width, bricks, result);
    return result;
}

private void waysOfBuildLayerRecursive(Stack<Integer> stack, int width, int[] bricks, List<Integer> result) {
    if (width == 0) {
        result.add(stack2int(stack));
        return;
    }
    for (int brick : bricks) {
        if (brick <= width) {
            stack.push(brick);
            waysOfBuildLayerRecursive(stack, width - brick, bricks, result);
            stack.pop();
        }
    }
    return;
}

private int stack2int(Stack<Integer> stack) {
    int result = -1;
    for (int brick : stack) {
        result++;
        result = result << (brick);
    }
    return result;
}