回归
回归
机器学习
寻找目标的重要的特征,并排序
机器学习其实是在做一个特征工程
深度学习目前成本很高
任务T
两类任务:分类、回归(连续空间)
多任务模型,把任务拆解
经验E
随着任务的不断执行,经验的积累会带来计算机性能的提升。
但也会出现过拟合
数据标记
性能P
一些技术性的评价指标:分类的准确率、模型的鲁棒性.
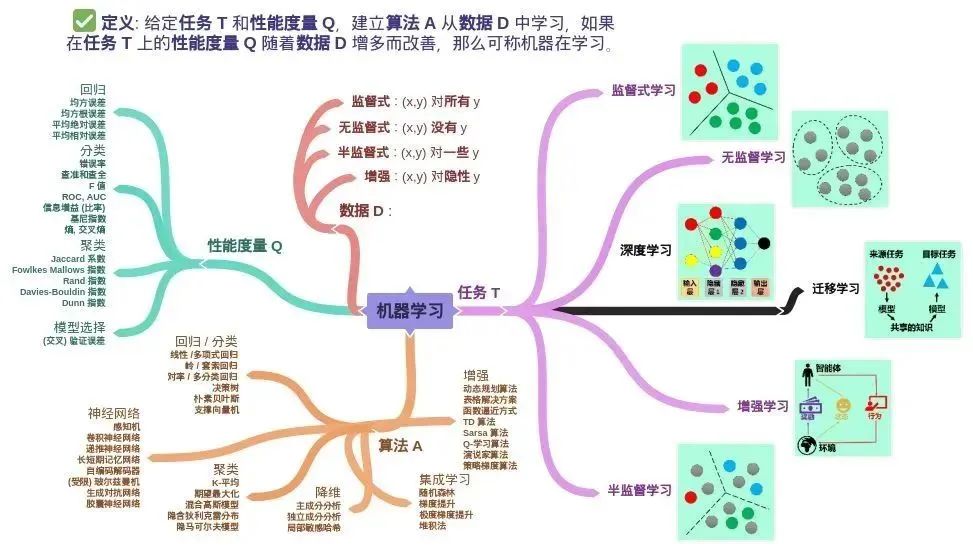
在该定义中,除了核心词机器和学习,还有关键词经验 E,性能度量 P 和任务 T。在计算机系统中,通常经验 E 是以数据 D 的形式存在,而机器学习就是给定不同的任务 T 从数据中产生模型 M,模型 M 的好坏就用性能度量 P 来评估。
由上述机器学习的定义可知机器学习包含四个元素
- 数据 (Data)
- 任务 (Task)
- 性能度量 (Quality Metric)
- 模型 (Model)
机器学习是一门让计算机从数据中学习规律和知识的科学。机器学习可以分为三大类:监督学习、无监督学习和强化学习。
监督学习是指根据已有的输入输出数据,训练出一个模型,用来预测新的输入的输出。例如,文字识别、图像分类、情感分析等。
无监督学习是指在没有输出数据的情况下,训练出一个模型,用来发现数据中的隐藏结构或模式。例如,聚类、降维、异常检测等。
强化学习是指在不断与环境交互的过程中,训练出一个模型,用来最大化累积奖励。例如,自动驾驶、游戏智能、机器人控制等。
难一点,用到深度学习的技术,但是独立于他们
机器学习有很多实例应用在各个领域,如自然语言处理、计算机视觉、生物信息学、推荐系统等。
线性模型
以波士顿房价预测为例
模型定义
变量一般定义如下:
- m: 训练数据的大小
- x: 变量,是一个向量,代表一个特征
- y: 变量,表示第i个训练的实例
初始值选取:用均值为0、方差0.1的正态分布去随机初始化,可以最大程度上避免陷入局部极小值。
构建一个线性模型,如下:
目标函数:即损失函数
利用随机梯度下降,最优化损失函数,设置一个更新次数,或者更新阈值
对损失函数求偏导数,结果如下
权值回归:线性回归的变种
根据中心极限定理,n个独立随机事件概率的和,应该符合正态分布,公式如下:
建立目标函数的方法:
- 最小二乘法
- 最大似然法/极大似然估计
极大似然估计,是机器学习里面建立目标函数更通用的思路:
利用概率论求解目标函数的方法更加通用
并且都会基于SGD去求解得到我们想要的模型
学习率,
逻辑回归
巧妙的使用一个线性模型去解决分类问题
模型定义
Sigmoid函数:
特性:
- 对称(奇函数)
- 大于0,快速的接近于1;小于0,快速的接近于0
属于广义线性模型:如果不把这个hx看作一个函数值,而是看作一个概率函数的话,他就是属于0分类或1分类的概率函数
在神经网络中,经常用做一个激活函数
损失函数/目标函数:
利用极大似然估计推到目标函数:
让他们概率最大
和线性模型的目标函数只差了一个负号,完全等价
单调性相同,目标函数就可以做等价处理
正则化
指数函数族
因为这两者是同一个族的,
逻辑回归的分界线,就是
高维空间的超平面,但是投影到二维平面上,会是曲线
低维问题难以找到分界线的话,可以考虑放到高维空间下去找,在高维度下可能就是线性可解的
问题:
- 计算不便
- 特征的差异性表达上不太好,可能分不清人和猴子
特征从低维到高维的方法
- 向量加几维度,用前面的自变量线性不相关的因素来表达
xyz甚至可以拓展成无限维的特征,分类效果有的时候也很好
在分界点上的点,本来就模棱两可,称为异质点,这个函数下没发具体分类,但是有的问题可以解决这个问题,就是异质点分类问题。
激活函数只能解决二分类问题
升维度,降维度
有不相关的,就可以加一个正则项,就是允许有一个tolerance存在
避免过拟合,方案
- 加正则项,
随机森林:有一定复杂度,但是没有很高的准确性。所以工程上现在基本就不用了
有监督分类器
把维度升的越高,分类分的越好
牛顿法的下降速度比梯度下降快很多,牛顿法是二次收敛
Hessian矩阵
如何判断想最小值还是最大值收敛:
通过二次导数判读
广义线性模型
求出一个概率分布,
常见分布:伯努利、伯松。都属于广义线性分布
然后利用最大似然法可以求的参数