Skip to main content

区块链技术发展进展-以认证数据结构为例

David LiuAbout 12 min

区块链技术发展进展-以认证数据结构为例

https://www.wwsww.cn/jishu/2081.htmlopen in new window

区块链技术发展概览

这部分主要参考这篇文章：

清华区块链报告：深度剖析国内外区块链最新进展 | 附报告全文 - 碳链价值 (ccvalue.cn)open in new window

三页左右即可，只是一个概述

区块链技术的发展，目前主要经历了1.0、2.0、3.0三次里程碑式的发展，

技术发展

应用发展

认证数据结构发展

概述

需要找几篇文献综述，主要参考如下：

高效验证的学术问题源于验证数据结构（ADS,authenticated data structure），即利用特定数据结构快速验证数据的完整性，实际上 MKT 也是其中的一种。为了适应区块链open in new window数据的动态性（dynamical）并保持良好性能，学术界展开了研究。Reyzin 等[[20](javascript:😉]基于 AVL 树形结构提出 AVL+，并通过平衡验证路径、缺省堆栈交易集等机制，简化轻量级节点的区块头验证过程。Zhang 等[[21](javascript:😉]提出 GEM2-tree 结构，并对其进行优化提出 GEM2כ-tree 结构，通过分解单树结构、动态调整节点计算速度、扩展数据索引等机制降低以太坊节点计算开销。

Authenticated data structures can be traced back to Merkle ²; the well-known Merkle hash tree can be viewed as providing an authenticated version of a bounded-length array. More recently, authenticated versions of data structures as diverse as sets ²¹, dictionaries ¹, range trees ¹, graphs ¹, skip lists ¹ have been developed.

树形结构

  • Merkle Tree 等

列举几种已经他们的特点，一到两页 PPT

非树形结构

列举几种已经他们的特点，一到两页 PPT

Efficient Set Accumulators

使用高效的集合累加器扩展可验证计算 |尤尼克斯 (usenix.org)open in new window

这个是本次分享的核心

原理概述

性能对比

代码实验

RSA accumulators are authenticated sets built from cryptographic assumptions in hidden-order groups such as mathbb {Z}_N^*. They enable a prover, who stores the full set, to convince any verifier, who only stores a succinct digest of the set, of various set relations such as (non)membership, subset or disjointness¹.

In other words, RSA accumulators allow you to prove that a value is part of a set without revealing the entire set. They are similar to Merkle trees but can be more efficient for certain use cases⁵.

分解

数论中最先讨论的问题就是分解.给一个合数 𝑁N,分解问题就是找出正整数 𝑝p,𝑞q 使得 𝑁=𝑝𝑞N=pq.尽管这面临的似乎是一个简单的问题,但事实上它是很难的,值得深入研究的问题.我们可以在指数时间检查所有的 𝑝=2,...,𝑁‾‾√p=2,...,N.然而解决问题在指数时间不是足够快的.尽管有多年的研究,还没有多项式算法可以解决分解大数的问题.很显然对 𝑁N 的某个特定的值很容易解决.例如 𝑁N 是偶数.但是,我们讨论的密码学构造中,𝑁N 是一个非常大的数,同时被连个大素数构造 𝑝,𝑞p,q.

RSA Accumulator

accumulator 是什么

A cryptographic accumulator is a one-way membership function. It answers a query as to whether a potential candidate is a member of a set without revealing the individual members of the set.

在密码学中，Accumulator 指的是一个能够在不暴露所有集合元素的情况下，配合证明(proof)确保某个元素在一个群集之中的单向函数。

Merkle tree 属于 Accumulator 吗？

是，也不是。

因为在已知 merkle root 情况下，配合 merkle branch 的关键路径作为 proof，我们就能证明一个元素的存在。

在严谨的密码学定义中，会要求 proof 是固定大小，而 Merkle tree 不符合此一定义。

那么如何保证 one-way membership function 呢？

密码学严重依赖于这样的假设，某些数学问题难以在有限的时间内解决。让我们看公钥(非对称)密码学，刚刚我们使用的一个假设-单向函数(One-Way function)存在。例如，一个函数在一种情况下很容易计算，而在另一种情况下不容易计算。我们使用数论算法来产生这样的函数，最典型的就是我们下面将要说的这个 RSA 算法的思路。

RSA 算法

密钥生成：

（1）任意选取两个不同的大素数 p 和 q 计算乘积

img

（2）任意选取一个大整数 e，满足

img

，整数 e 用做加密钥（注意：e 的选取是很容易的，例如，所有大于 p 和 q 的素数都可用） [5] ；

（3）确定的解密钥 d，满足

img

，即

img

是一个任意的整数；所以，若知道 e 和

img

，则很容易计算出 d [5] ；

（4）公开整数 n 和 e，秘密保存 d [5] ；

加解密算法：

  • c=E(m)=memod  nc=E(m)=m^e\mod n
  • m=D(c)=cdmod  nm=D(c)=c^d\mod n

然而只根据 n 和 e（注意：不是 p 和 q）要计算出 d 是不可能的。因此，任何人都可对明文进行加密，但只有授权用户（知道 d）才可对密文解密。

RSA 公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

RSA 问题

在 RSA 公钥加密中，Alice 使用 Bob 的公钥(n,e)加密明文 M 生成 C，计算方法为C=Memod  nC=M^e \mod n,其中 n 是由两个大素数产生的,e≥3 并且是一个奇数且和 Zn∗ 互质,Zn。Bob 知道私钥(n,e)，其中

de=1mod  ϕ(n)de=1\mod\phi(n)

(p−1)(q−1)(p−1)(q−1)

意味着 M=Cd(mod n)。攻击者能够窃听 C 同时知道公钥(n,e)。然而为了计算 M，攻击者必须找到 n 的分解。因此，这意味着 RSA 问题并不比整数因子分解困难，但是如果选择合适的 n，这仍然是一个很难解决的问题。

RSA 问题是在给定 RSA 公钥(n,e)和密文C≡Pemod  NC≡P^e\mod N的情况下有效地计算P。

RSA 公钥的结构要求 N 是一个大的半素数（即两个大素数的乘积），2 < e < N，e 是 ϕ(n)\phi(n)（欧拉函数，在数论，对正整数 n，欧拉函数是小于 n 的正整数中与 n 互质的数的数目）的互质数，0 ≤ C < N。 C 在该范围内随机选择；要完全精确地指定问题，还必须指定如何生成 N 和 e，这将取决于所使用的 RSA 随机密钥对生成的精确方法。

The RSA Problem: Given an RSA public key (n,e) and a ciphertext C=Me (mod n),to compute M. 即攻击者不知道 RSA 私钥但是仍要反求 RSA 函数来得到明文。

RSA 假设

当 n 充分大且随机取的时候，认为 RSA 问题难以解决。

即认为 RSA 函数是一个单向陷门函数。

为什么要充分大呢？

明文取值空间要足够大且随机，否则攻击者可以通过遍历来进行攻击

一般来说，为提高保密强度，RSA 密钥至少为 500 位长。

RSA-2048具有617个十进制数字，共2048bits。是目前最大的RSA数字。

强 RSA 假设

在密码学中，强 RSA 假设指出，即使允许 solver 选择公共指数 e（对于 e ≥ 3），RSA 问题也是棘手的。也就是说，给定未知因式分解的模 N 和密文 C，找到任何使 C ≡ M e mod N 的对 (m, e)是不可行的。

该假设与 RSA 假设的不同之处在于对手可以选择公开指数 e。攻击者目标为在给出密文 C，模数 n 后计算任意一个满足 C=Me(modn) 的公开参数 e（奇数且 e>3 ）和明文 M。这可能比解决 RSA 问题更容易，所以这个假设是比 RSA 假设更强的假设。强 RSA 假设是各种加密构造的基础。

https://zhuanlan.zhihu.com/p/618253489open in new window

RSA Accumulator

它的基本数学非常简单，我们透过一个质数 g 作为基底，再配合一个选择好的 N = p * q ，其中 p,q 皆为秘密的大质数。

  1. 利用上述 RSA 选择 N 的策略，生成两个大质数 p, q 得到 N
  2. 选择一个基地 g

N Value Setup

首先必需介绍一下 N 的选择。 N 是由两个秘密质数相乘而来，若有人知道其组成，将可以破解 RSA Accumulator 的验证。因次对于 N 的选择，可以选择相信公开宣布已经销毁 p, q 的 N 值，或是 RSA2048 这种目前技术进行分解的大数。另一个可行的方法是透过所谓的 Class Group 来进行 N 的创造，但这方面牵扯很多复杂的数学，有兴趣的人可以自己参考这篇论文。

Initiation

当我们选好了基底 g 想要创建一个 Accumulator，

放入数字 a 的时候，就进行 gag^a 次方运算，得到 Accumulator A。

A=gamod  N A = g^a \mod N

若是要加入新的成员到 Accumulator 中，就继续执行次方运算。例如我们接着想要加入 a2,a3a_2, a_3，那么我们的 Accumulator 就会变为：

A=A(a2×a3)mod  N=g(a×a2×a3)mod  N A = A^{(a_2 \times a_3 )} \mod N= g^{(a\times a_2\times a_3)} \mod N

Membership Witness

若我们想要证明 a1a_1 确实在这个 Accumulator 之中，我们需要提供的 witness w 就是 Accumulator 扣除了 a1a_1 的部分，验证则是试算 wa1w^ {a_1} 是否等于 Accumulator 的值。

w=g(a2×a3)mod  Nw = g^{(a_2 \times a_3)} \mod N
verify:A=wa1mod  N: A = w^{a_1} \mod N

举一个直观的数字例子（先忽略 mod N）：

我们可以发现，不论现在 Accumulator 已经存放的多少东西，都可以透过在只知道 Accumulator 目前 root value 的情况下，以 O(1)的复杂度加入元素。这样的 Accumulator 称为 Dynamic Accumulator，广泛一点来说就是能够随意 Update 这个 Accumulator。

Aggregating Proofs

若我们想要证明{a1,a2,a3}\{a_1,a_2,a_3\}都在Accumulator中，我们可以把证据合并在一起提供一个witness w，就是去除了待证明的集合中的元素。

w=g(a4×a5...)mod  Nw = g^{(a_4 \times a_5...)} \mod N
verify:A=wa1×a2×a3mod  N: A = w^{a_1\times a_2\times a_3} \mod N

除此之外，我们还可以把多个想要验证的值，合并在一起产生一个 witness。例如下图例子中，我们可以一次验证 5, 13 都在 Accumulator 中。

这种能整合多个 witness 为一的特性称为累加性 (Aggregating)。而有效率的一次产生或验证多个 witness 则称为批次性 (Batching)。这两者都是 merkle tree 不具备的。

优化

朴素地计算所有n个成员身份见证人需要O（n2）的幂𝔾，这不能很好地在大规模场景下计算。Sander等人给出了一种计算所有见证人的分治方法。

关键的观察结果是，一半的见证人需要计算gπi∈[1，n/2]ei，而另一半则需要计算g∏i∈[n/2+1，n]ei。如果做得很天真，这些计算会重复很多次，这是不必要的。但是可以以如下树状方式递归地计算见证人（在本例中n＝8）：

直觉：你可以把每个节点想象成（1）一组元素，（2）它的批成员身份见证器w.r.t.累加器a。然后，这个算法简单地把集合分成两半，并把见证分解成两半的见证器。这种情况一直重复，直到在底部获得单个元素的见证。

Non-Membership Witness

验证方法会需要用到裴蜀定理(Bézout's identity)：

ax+by=max + by = m
(x, y)有整数解时若且唯若m是(a,b)的最大公因数d的倍数。

也就是说：ax+by=1ax + by = 1
(x, y)有整数解时若且唯若(a,b)互质。

RSA Accumulator 除了能够的验证一个 element 在一个 Accumulator 中外，也能够进一步给出非成员证明(non-membership witness)，及证明一个数字不存在此 Accumulator 中。

用上面的例子来看，假如果要证明数字 7 不是 1105 因数，根据贝祖定理，我们只要找到一组满足 7a + 1105b = 1 的整数解即可（可以用 exgcd 算法去求解）。完整的过程如下：

img

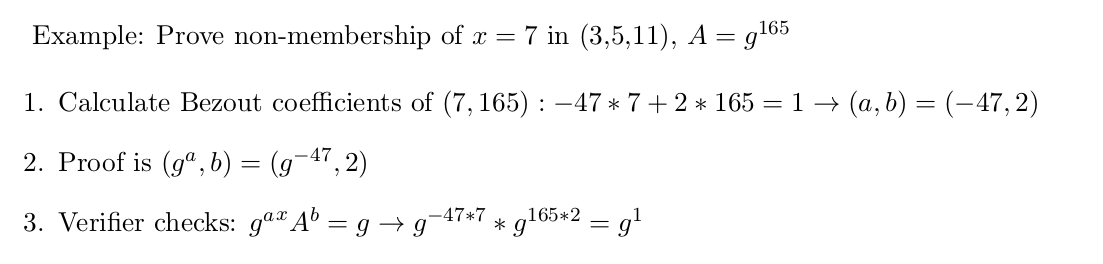
例如，试证明7不存在于(3,5,11)中

  1. A=g165A=g^{165}
  2. 计算7a+165b=17a+165b=1的整数解（如利用拓展欧几里得算法），得到(-47, 2)
  3. 证据就是(ga,b)=(g−47,2)(g^a,b)=(g^{-47},2)
  4. 验证者只需要检查：gaxAb→g−47×7×g165×2=g1g^{ax}A^b\rightarrow g^{-47\times7}\times g^{165\times 2}=g^1

Batching non-membership witnesses

证明{x1,x2,...,xm}\{x_1,x_2,...,x_m\}不在集合中。

令x∗=∏i=1mxix^*=\prod_{i=1^mx_i}，证明gcd(s∗,x∗)=1gcd(s^*,x^*)=1，并给出一组整数解作为证据

Proof of Knowledge Schemes

现在我们已经知道 RSA 如何进行验证，基本上就是次方的运算。但这在实践上有个困难点，因为若是结合了许多要验证的值的话，x 的大小会线性成长，因此我们不会直接提供 x ，而是需要再透过其他 proof of knowledge scheme 来间接完成。

我们可以把问题简化成：已知 u ^ x = w ，如何在不实际运算 u^x 的情况下验证这件事情。以下我们举一个简单例子：Proof of Exponentiation。

img

Proof of Exponentiation

透过这个 Scheme，最后 proof 大小上会因为 x/B 的步骤而限缩。而验证时，虽然需要 Verifier 自己算出 r = x mod B ，不过在 RSA 的使用情境中会比算次方快上许多。

在 Georgios Konstantopoulos 的 A Deep Dive on RSA Accumulator 这篇文章中更仔细的介绍了不同 Proof of Knowledge Scheme 如何配合 RSA Accumulator 进行 membership 以及 non-membership 的验证，就留给对数学更有兴趣的人自己看啦。

相比于Merkle Tree好处

  • 批量证明
  • Proof大小不随验证成员数增加。
  • 不需知道所有State也能进行更新。

BenchMark

与Merkle Tree性能对比：

参考文献

  • Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains, by Dan Boneh and Benedikt Bünz and Ben Fisch, in Cryptology ePrint Archive, Report 2018/1188, 2018
  • A Deep Dive on RSA Accumulator
  • Scaling Verifiable Computation Using Efficient Set Accumulators
  • Authenticated Data Structures, Generically
姓名工作贡献
刘大维文献收集、拟定大纲、RSA Accumulator、代码复现、性能对比、讲稿与展示
郑晨枫认证数据结构概述、树形结构
张国庆非树形结构
郭子恒区块链技术发展与应用场景概述
David's Blog
Copyright © 2024 David Liu