Rigging, Binding, Skinning

• Rigging
• Binding
• Skinning

Transform Blend

Bind Pos

• T Pose
• A Pose

Binding

However, since each vertex has only one influencer, the deformation will exhibit sharp transitions around rotating joints.

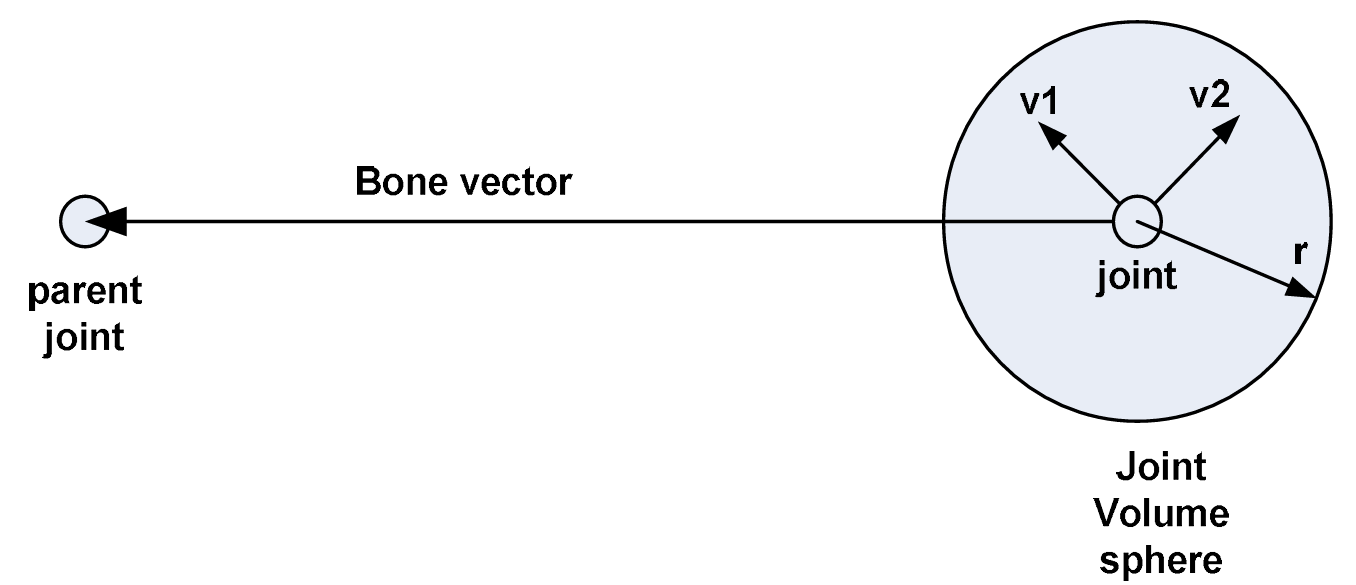
To allow multiple joints to influence a vertex, we need to define volume spheres within which a vertex can be influenced by both its nearest joint and the nearest joint's parent

Precomputing the radii of each joint’s volume sphere 1. 2. Find the nearest vertex for each joint (instead of nearest joint to each vertex) Create an array containing the nearest vertex distances to each joint (array length should correspond to the number of joints).

Unfortunately these distances cannot be used directly as the radii of the volume spheres, since the result would include only one vertex in each sphere. Instead, multiply these distances by a radius multiplier, preferably around 1.5 or 2, then store them in the array Note: If the radius multiplier is too large, it may include irrelevant vertices in the sphere, leading to visual artifacts during deformation.

Skinning

steps

1. bind matrices

   $v_b^i=F_0^iv_b^0$

   $B_0^i=(F_i^0)^{-1}$

2. Compute the new vertex position

3. Deform

LBS: Linear-Blending

$v^0=\sum w_iH_i^0(\theta)B_iv_b^0$

for (int i = 0; i < vertex.getInfluenceCount(); i++)
{
    int jointIndex = vertex.getJointIndex(i);
    double weight = vertex.getJointWeight(i);

    ATransform jointTransform = this->jointGlobalTransforms[jointIndex];
    ATransform bindMatrix = this->bindMatrices[jointIndex];

    ATransform combinedTransform = jointTransform * bindMatrix;

    outputPosition += weight * combinedTransform.RotTrans(vertex.getPosition());
    outputNormal += weight * combinedTransform.Rotate(vertex.getNormal());
}

outputNormal = outputNormal.Normalize();

DQS: Dual-Quaternion

quat blendedReal(0, 0, 0, 0);
quat blendedDual(0, 0, 0, 0);

for (int i = 0; i < vertex.getInfluenceCount(); i++) {
    int jointIndex = vertex.getJointIndex(i);
    double weight = vertex.getJointWeight(i);

    quat realPart = this->reals[jointIndex];
    quat dualPart = this->duals[jointIndex];

    // Ensure shortest arc for real quaternion blending
    if (quat::Dot(blendedReal, realPart) < 0.0f) {
        realPart = -realPart;
        dualPart = -dualPart;
    }

    blendedReal += weight * realPart;
    blendedDual += weight * dualPart;
}

double realLen = blendedReal.Length(); 
blendedReal = blendedReal / realLen;
blendedDual = blendedDual / realLen;

ATransform combinedTransform;
this->convert(blendedReal, blendedDual, combinedTransform);

outputPosition = combinedTransform.RotTrans(vertex.getPosition());
outputNormal = combinedTransform.Rotate(vertex.getNormal()).Normalize();

Binding

Determine weight of joint i and joint j.

1. finding the nearest joint (J1) for a vertex V (V1 or V2)
2. create a vector from the nearest joint to the vertex, and another vector from the nearest joint to its parent.
3. Project the vertex vector onto the bone vector using the dot product and check the sign of the result.
   1. A negative value (for V1 in the above image) indicates that the projection is in the opposite direction, meaning V1 should be influenced by the nearest joint J1
   2. A positive value (for V2 in the above image) indicates that the projection is along the bone vector, meaning V2 should be influenced by the nearest joint's parent, J2.

Find the nearest vertex for each joint (instead of nearest joint to each vertex)

Create an array

compute bone vector representing distance joint and angles