Interpolation
Interpolation
Lengyel Chep 11.1-11.3
Single curve => global scheme
precises curve => local scheme
Explicit
Curves Representation
Three ways
Explicits
Example:
properties
- generative
- Can only represent single-valued functions
Implicit
Example:
Properties
- Non-generative
- Can represent multi-valued functions
Parametric
where u is independent variable
Example:
Properties:
- generative
- Can represent multi-valued functions
- Different parametrization can produce the same path
Curves
Polynomial Curves
Monomial Form
where n=degree of polynomial curve (highest exponent)
- Linear
- Quadratic
- Cubic
=>monomial form
Example
Derivative
Continuity of Curves
not continuous 不连续
自己连续,导数不连续
一阶导数连续,后面不连续
二阶导数连续,后面不连续
Note: Human visual system cannot distinguish discontinuities greater than to 2
Interpolation
General form (of curve and )
Basis functions of degree n (scalars not matrix)
Monomials:
Linear Interpolation (n = 1)
Bézier curves
General form
n=1, linear
n=2, quadratic
n=3, cubic
General Form of Bernstein Polynomials of degree n
control points
control points
b1, b2: slope
b0, b3: point
让两个 curve 连接处平滑
几何意义:控制点就是这个曲线的 Convex Hull
Review, Lecture 7
Cubic Polynomials
monomials
Constructing Bezier Curves
De Casteljau Algorithm
Computes Bezier curve function using successive linear interpolation
eg. want to know value of curve at u=0.25
where,
Systolic(收缩) Array – associated with calculation of intermediate control points
Subdivision of Bezier Curve
Derivatives
case n=3
Therefore,
Splines
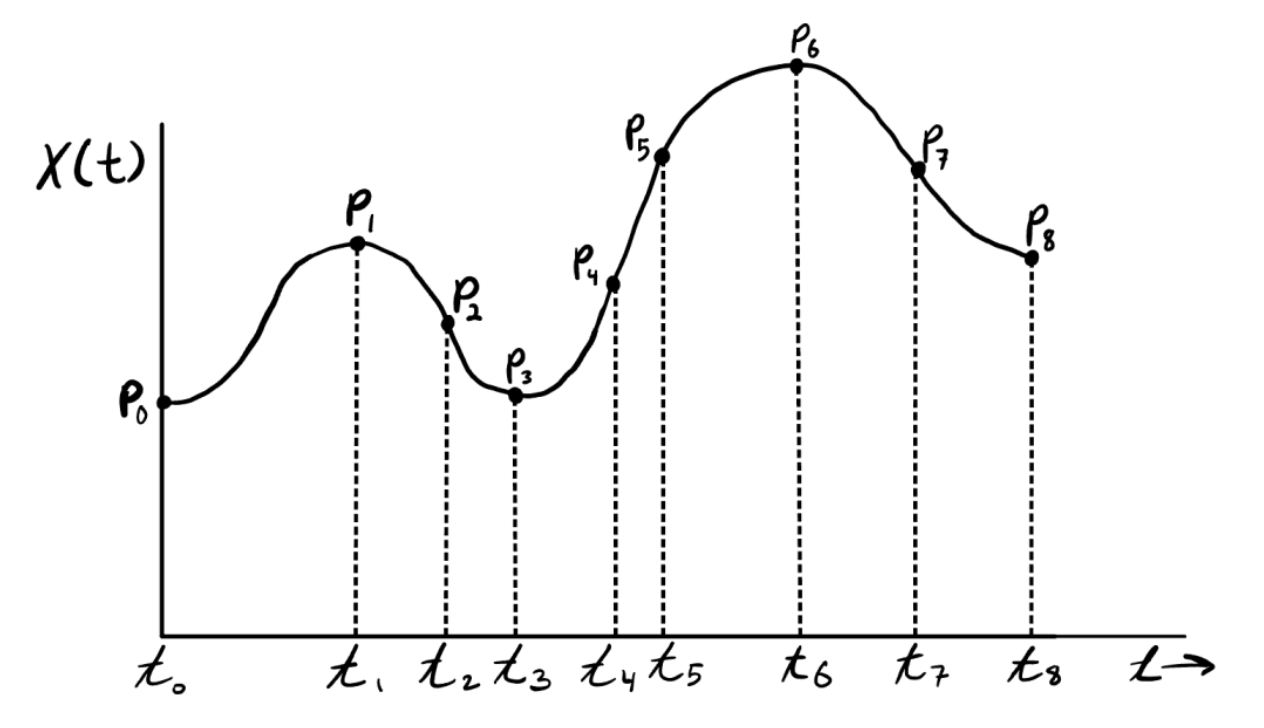
Notations
: the knots of spline
: # of curve segments
: degree of the curve segments
number of points
Objective
Given
- a set of points
- basis function polynomials of degree n
find the coefficient for the curve segment of the spline
Catmull-Rom Splines
Centrol point: slope between two segment is same
C1 continuity
Use Bezier curves for each segment
Cubic splines (n=3)
Control Point Array
Collect all the control points for spline into an array
Computing control points for each curve segments (n=3, case)
Central difference
平均值 assume
Endpoint
对于左右端点,特别的定义
Left:
Right:
point value
to evaluate curve segment's particular point value in time t, need to compute B
- Compute u,
- Use Bernstein polys to evaluate B
or
De Casteljau Algorithm
Monomial Formulation for cubic curves
m the Monomial form
Bezier Curve
What if I give the monomial coefficients () and value of
Hermite Curve
reworked Bezier curves
- : left side of curve
- : right side of curve
- : slope of left side of curve
- : slope of right side of curve
What is the basis functions H
Bezier curve derivatives
Hermite Spline
C2 continuity
General Case
1st Derivative:
2nd Derivative:
To have continuous 2nd derivative between segments
Constraint
AC=D, C=A^{-1}D
Endpoint
Clamped Endpoint Conditions
S0, sn
natural spline
left and right side of curve 2nd derivative = 0
Spherical Interpolation (Slerp)
Interpolating Quaternion
linear combination of q1, q2
=>
let
Quaternion Splines
Cutmal-Rom
- slerp
- sdouble
- sbisect
use de Casteljau to evaluate spline at a given u
Statement
Assume want the equivalent of a Catmull-Rom spline
bezier
Geometric Interpretation of slope
Introduce 3
Operators
left slope
=>
right slope
=>
Applied to circle
Operators
Cubic Splines
where
edge case
Cubic Quaternion Catmul-Rom Splines
de Casteljau algorithm
Shape Animation
2D Surfaces
surface
two tengant
normal:
Bilinear surface patch
2D linear interpolation
General form of Bilinear interpolation
2D Cubic Bezier
FFD (Free Form Deformation)
Jaccob matrix
